Integrate tan^2x sec^2x/1-tan^6x 265185

Integrate 2x sin (x 2 1) with respect to x Solution We know that the derivative of (x 2 1) = 2x Hence, let's substitute (x 2 1) = t, so that 2x dx = dt Therefore, ∫ 2x sin (x 2 1) dx = ∫ sin t dt = – cos t C = – cos (x 2 1) C Example 3 Integrate {(tan 4 √x) (sec 2 √x)}Answer and Explanation 1 Given integral ∫ tan3(x)sec2(x)dx ∫ t a n 3 ( x) s e c 2 ( x) d x To evaluate this integral, we make the substitution u =tan(x) u = tan ⁡ ( x) ThisTo integrate 2sec^2x tanx, also written as ∫2sec 2 x tanx dx, 2 sec squared x tan x, and 2(sec x)^2 tanx, we start by recognising that the differential of one half is within the other half of the same expression In this case, the differential of tanx is sec squared x, which should fill you with great confidence to use the u substitution method

Solved 9 Integral Tan 3xsec 4xdx Integral Chegg Com

Integrate tan^2x sec^2x/1-tan^6x

Integrate tan^2x sec^2x/1-tan^6x-Question Evaluate the integral ∫ tan4x sec6x dx Explanation A Explanation B Explanation C Question ∫ tan ⁡ 4 x s e c 6 x d x \int \tan^ {4}x sec^ {6}x dx ∫ tan 4 x se c 6 x d x =Exercises More on USubstitution Integrate ∫ 4 x2 6x 9 dx ∫ x2 (x3 − 1)2 dx ∫ x2 x3 − 1 dx ∫ x √1 − 4x4 dx ∫ x3 √1 − 4x4 dx ∫cos(4x) dx

Int Tan 2xsec 2x 1 Tan 6x Dx Youtube

 For the first integral, substituting u = tanx, du = sec^2 (x) dx which takes care of the right half of it Now for the second integral from several steps above Breaking it down to take out a tangent to get a tan squared Using the trig identity for tan squared Distribute the tan Break this into another two integralsIntegral of Tangent to the Sixth Power (tan^6 (x)) by Mark (US) Here's another example submited and solved by Mark Here we just use the technique described when we have tangent and secant We just do the basic substitutions Return to Trigonometric Integrals Click here to post commentsGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!

 Integral (1 tan^2(x))/sec^2(x)integrating powers of tangent and secantAnswer (1 of 5) Let T = \displaystyle \int \frac{\sec^3{x}}{\tan^2{x}} \,\mathrm dx Recall that \sin^2{\theta} \cos^2{\theta} \equiv 1\ \therefore \cos^2{\theta Ex 71, 19 sec 2 2 dx sec 2 2 = 1 cos 2 1 sin 2 = 1 cos 2 sin 2 1 = sin 2 cos 2 = tan 2 = sec 2 1 = sec 2

 In (tan^2)x your 1st mistake is not writing dx Note that dx is NOT always du!!!!!X = 1 u 2 See Example 1814 When m m is even and n = 0 n = 0 — that is the integrand is just an even power of tangent — we can still use the u = tanx u = tan ⁡ x substitution, after using tan2x= sec2x−1 tan 2 ⁡ x = sec 2 ⁡ x − 1 (possibly more than once) to create a sec2x sec 2 To evaluate this integral, let's use the trigonometric identity sin2x = 1 2 − 1 2cos(2x) Thus, ∫sin2xdx = ∫(1 2 − 1 2cos(2x))dx = 1 2x − 1 4sin(2x) C Exercise 723 Evaluate ∫cos2xdx Hint cos 2 x = 1 2 1 2 cos ( 2 x) Answer ∫ cos 2 x d x = 1 2 x 1 4 sin ( 2 x) C

2

Integral Of Tan 2 X Sec X Youtube

Answer We can immediately cancel \sec^2 x from both sides to get \sec^2 x \tan^2 x = \tan^2 x \tan^4 x Or \displaystyle \frac{1}{\cos^2 x}{\sin^2 x}{\cos^2 x} = \frac{\sin^2 x}{\cos^2 x} \frac{\sin^4 x}{\cos^4 x} Now notice that if \sin x = 0 the equation is trivially satisfied, so letSec(x) tan(x) dx = Z 1 sec(x) tan(x) sec2(x) sec(x)tan(x) dx = Z 1 u du for ˆ u= sec( x) tan( ) du= (sec2( x) sec( )tan( ))dx = lnjuj C = lnjsec(x)tan(x)j C Another trick for this is to write R sec(x)dx= R 1 cos2(x) cos(x)dx, and substitute u= sin(x) to get R 1 1 u2 du We will see how to integrate such rational functions in x74Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more

Int Tan 2xsec 2x 1 Tan 6x Dx Tan2 X Sec

Qprove That Tan X 2 Tan 2x 4 Tan 4x 8 Cot 8x Cot X Mathematics Topperlearning Com Blpusg55

\\int \tan^{2}x\sec{x} \, dx\ > <∫tan3 xsin2 3x(2 sec2 xsin2 3x 3 tan x sin 6x) dx for x ∈ π/6,π/3 is equal to (1) 9/2 (2) 1/9 (3) 1/18 (4) 7/18 That is, we have tanx in squared form accompanied by its derivative, sec2x This integral is ripe for substitution!

Integral Of Sec 6 X Tan 2 X Dx

bestpictjcry Tan 2x Tan 2x

Problem Find $\displaystyle\int \frac {\tan 2x} {\sqrt {\cos^6 x \sin^6 x}} dx $ Solution $\tan 2x= \dfrac{2\tan x}{1\tan^2 x}$ Also I can take $\cos^6x$ common from $\sqrt {\cos^6x \sin^6x}$ I don't know whether it is good approach to the question Please helpTo avoid ambiguous queries, make sure to use parentheses where necessary Here are some examples illustrating how to ask for an integral integrate x/(x1) integrate x sin(x^2) integrate x sqrt(1sqrt(x)) integrate x/(x1)^3 from 0 to infinity; You don't need to remember complicated formulas just recall secx = 1 cosx, tanx = sinx cosx so your integral is ∫ sinx cos3xdx = ∫ − 1 t3dt with the substitution t = cosx Share answered Sep 15 '15 at 1331 egreg egreg 2k 17

Integration Trig Identities Ppt Download

How To Prove That Lhs Rhs Sin2x 2tanx 1 Tan Square X Quora

Answer to Integrate the trigonometric integral integral of sec^2(x)/(1tan(x)) dx evaluated from 0 to pi/4 By signing up, you'll get thousands ofIntegral of sec^6 x/tan^2 x dx trigonometry formulae integration formulae Articles index Some things to do with your old computer Hosted by wwwGeocitieswsMATH 142 Trigonometric Integrals Joe Foster Example 1 Find ˆ sin3(x)dx Here we have an odd power of sin(x), so we are in case 1The idea then is that we want to peel away one of the sin(x) terms and then use the identity sin2(x) = 1− cos2(x) on the ones that are leftSo,

What Is The Integral Of Tanx Sec 2x 1 Tan 2x Quora

Int Tan 2xsec 2x 1 Tan 6x Dx Youtube

See all questions in Integrals of Trigonometric FunctionsHow do I evaluate the indefinite integral #intx*sin(x)*tan(x)dx# ?2 If n is odd, then using substitutions similar to that outlined above we have ∫sinmxcosnx dx = ∫um(1 u2)k 𝑑u, where u = sinx and du = cosx dx 3 If both m and n are even, use the halfangle identities cos2x = 1 cos(2x) 2 and sin2x = 1 cos(2x) 2 to reduce the degree of the integrand

Evaluate Int Tan 2xsec 2x 1 Tan 6x Dx

Sec 6x Tan 6x 1 2 Tan 2x Sec 2x Important Difficult Trigonometric Identity Youtube

1 Answer1 Active Oldest Votes 2 You can always decide whether an indefinite integral is correct by differentiating the answer to see whether you get back the original function So, differentiate your answer do you get tan 2 ⁡ x sec ⁡ In this section we look at integrals that involve trig functions In particular we concentrate integrating products of sines and cosines as well as products of secants and tangents We will also briefly look at how to modify the work for products of these trig functions for some quotients of trig functions Integrate $$\int \tan^6x\sec^3x \ \mathrm{d}x$$ I tried to split integral to $$\tan^6x\sec^2x\sec x$$ but no luck for me Help thanks

Integration Trig Identities Ppt Download

What Is The Integral Of Int 3x 1 2x 2 6x 5 Dx Socratic

Integrate x^2 sin y dx dy, x=0 to 1, y=0 to pi;Remember that $\sec^2(x) = 1 \tan^2(x)$ Hence the integral $$I = \int \tan^4(x) \sec^6(x) dx = \int \tan^4(x) \sec^4(x) \sec^2(x) dx\\ = \int \tan^4(x) \left(1 \tan^2(x) \right)^2 \sec^2(x) dx $$ Let $\tan(x) = t$Integration of tan^2x sec^2x/ 1tan^6x dx Ask questions, doubts, problems and we will help you

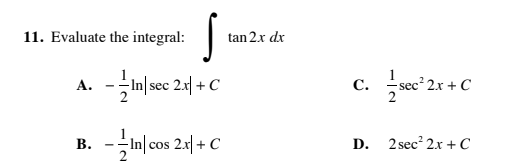
Answered 11 Evaluate The Integral Tan 2x Dx A Bartleby

Solve Tan 1 1 1 2x Tan 1 1 1 4x Tan 1 2 X 2

 63 Trigonometric Integrals Integrals of the form ∫ sin ( m x) sin ( n x) d x, ∫ cos ( m x) cos ( n x) d x, and ∫ sin ( m x) cos ( n x) d x Integrals of the form ∫ tan m x sec n x d x Functions involving trigonometric functions are useful asAnswer (1 of 3) Let u = tan x, du = (sec x)^2 dx, while (sec x)^4 = 1 (tan x)^2^2 = (1u^2)^2 Thus, by substitution, we can simply the integral as = Int u^2 (1 u^2)^2 du = Int (u^6 2u^4 u^2) du = (1/7) u^7 (2/5) u^5 (1/3) u^3 C = (1/7) (tan x)^7 (2/5) (tan x)^Tan^2xsec^2x/1tan^6x Ask questions, doubts, problems and we will help you

Ex 7 3 15 Integrate Tan3 2x Sec 2x Class 12 Ncert Ex 7 3

Solved 9 Integral Tan 3xsec 4xdx Integral Chegg Com

If k k is even and j j is odd, then use tan 2 x = sec 2 x − 1 tan 2 x = sec 2 x − 1 to express tan k x tan k x in terms of sec x sec x Use integration by parts to integrate odd powers of sec x sec xAnswer to Integrate the following 1 csc^3(x)dx 2 tan^3(2x)sec^3(2x)dx 3 sin(6x)cos(2x)dx 4sin(6x)cos(2x)dx 5 sin^4(3x)cos^3(3In the integral ∫tan2xsec2xdx, let u = tanx and du = sec2xdx This gives us ∫tan2xsec2xdx = ∫u2du Performing this integration yields u3 3 C, and since u = tanx, this becomes tan3x 3 C Answer link

Tan2x ただの悪魔の画像

Int Tanx Sec 2x Sqrt 1 Tan 2x Dx

The formula sin 2(x) cos2(x) = 1 and divide entirely by cos (x) one gets tan 2 (x) 1 = sec 2 (x) One case see that in the case where you have an even (nonzero) power of sec(x) the rst is possibleLet, u = (tanx)^2 and v = (cosx)^2 Now differentiating u and v with respect to x Then du/dx = 2 tanx (secx)^2 And dv/dx = 2 cosx(sinx) Now (du/dx)÷(dv/dx) = du/dvIntegrate 1/(cos(x)2) from 0 to 2pi;

Tan2x Sec2x ただの悪魔の画像

Tan2x Sec2x ただの悪魔の画像

We can also figure out a formula for integrals of powers of tangent Z tan k (x) dx = tan k1 (x) k1Z tan k2 (x) dx To do this, we'll use the fact that tan 2 (x) 1 = sec 2 (x) 72 Integral of Secant derivation Let's check out the fabulously clever trick for finding the integral of secantIntegral of tan^2 (x) \square!Integral of sec^3x https//wwwyoutubecom/watch?v=6XlSP58uisintegral of sec(x) https//wwwyoutubecom/watch?v=CChsIOlNAB8integral of tan^2x*secxintegral

Solved 1 Differentiate The Following With Respect To X Y Chegg Com

Integration By Parts X 𝑒ˣdx Video Khan Academy

X by the substitution of dx, d x, and be left with an even number of secants Use sec2x = 1tan2x (= 1u2) sec 2 ⁡ x = 1 tan 2 ⁡ x ( = 1 u 2) to replace the leftover secants The power of tangent is odd (n n odd) Use u = secx u = sec ⁡ How do I evaluate the indefinite integral #int(tan^2(x)tan^4(x))^2dx# ? The answer is =ln(tanxsecx)sinxC "Reminder" intsecxdx=ln(tanxsecx)C Therefore, the integral is int(tan^2xdx)/(secx)= intcosxtan^2xdx =intcosx(sec^2x1)dx =int(secxcosx)dx =ln(tanxsecx)sinxC

Integral Of Sec 2 X Sqrt 1 Tan 2 X Using The Arcsine Function Youtube

Q45 Integral Of 1 Tan 2x Sec 2x Youtube

Sol I= ((1tan^2 x ) tanx )dx /((1cot^2 x ) cotx ) I=(sec^2 x tanx )dx/ (cosec^2 x cotx ) I=(1/cos^2 x sinx /cosx)dx /(1/sin^2 x cosx /sinx ) I={(1sinxIf you let u=tanx in integral (tan^2)x you get integral u^2 dx which is not (u^3)/3 c since du= sec^2x

1

いろいろ Tan2x 1sec2x ただの悪魔の画像

How Do You Integrate 1 Tan2x Sec2x Dx Socratic

Evaluate The Integral Integral 0 Pi 6 8 Sqrt 1 Cos 6x Dx Study Com

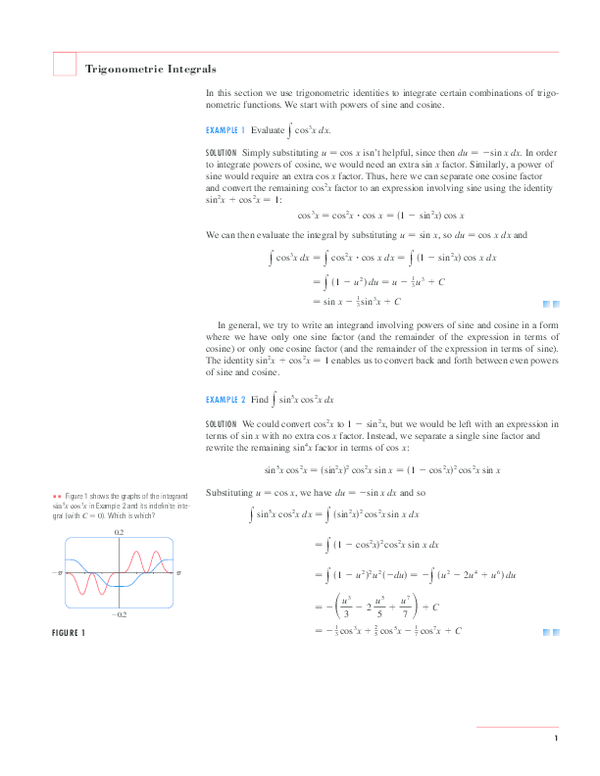
Pdf Trigonometric Integrals Jerome Delen Academia Edu

Solved Prove That Tan 8x Tan 6x Tan 2x Tan 8x Tan 6x Tan 2x

いろいろ Tan2x 1sec2x ただの悪魔の画像

Evaluate The Following Integrals Sec 4 2x Dx Sarthaks Econnect Largest Online Education Community

最も選択された Tan 2x Sec 2x 1 9959 5

How Do You Integrate 6x 1 X 2 2x 3 Socratic

Tan2x Sec2x ただの悪魔の画像

2

いろいろ Tan2x 1sec2x ただの悪魔の画像

2

How To Integrate Math Tan 2 X Sec 6 X Math Using U Substitution Quora

Solved 12 Evaluate The Integral Tan 2x 1 Sec 2x 1 Dx Chegg Com

Solved 16 Integrate Dx A Xº Sin 4x Dx B 4xcosh 3x Dx Chegg Com

Integral Of Cos 2x Tan 4x

Integral Of Tanx 2 Secx

Midterm 17 18 Questions And Answers Studocu

Prove Identity Sec 6x Tan 6x 1 3tan 2xsec 2x Brainly In

bestpictjcry Tan 2x Tan 2x

Solved Evaluate The Following Integral Sec 2x Tan 2x Dx Sec Chegg Com

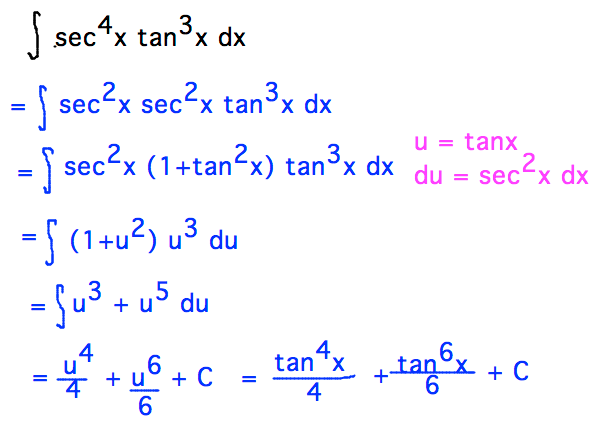
Geneseo Math 222 01 Trigonometric Integration

Solved Find The Indefinite Integral Use C For The Constant Chegg Com

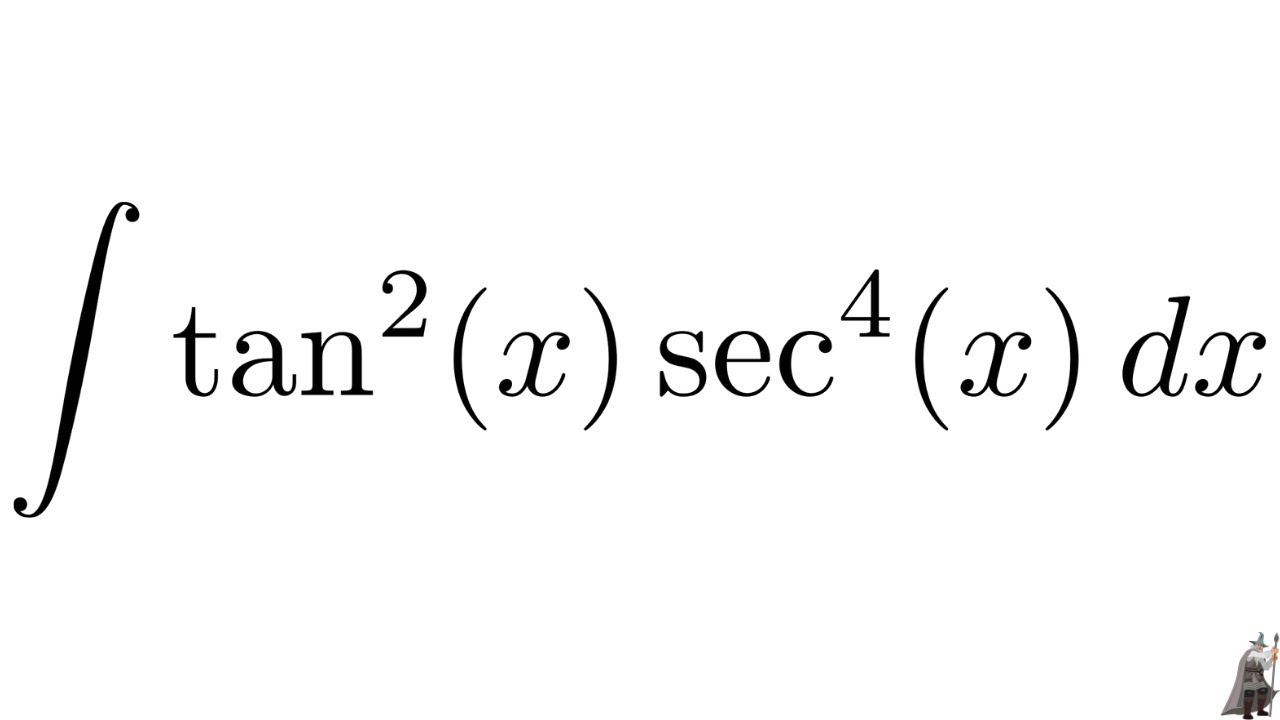
Integral Tan 2 X Sec 4 X Youtube

How Do You Integrate Csc2x Cot2x 2 Dx Socratic

Ex 9 4 4 Find General Solution Sec2 X Tan Y Dx Sec2y

1

Solved Evaluate Integral Tan 6 2x Sec 4 2x Dx If We Chegg Com

1 Tan 2 X Sec 2 X

7 2 Trigonometric Integrals Ppt Download

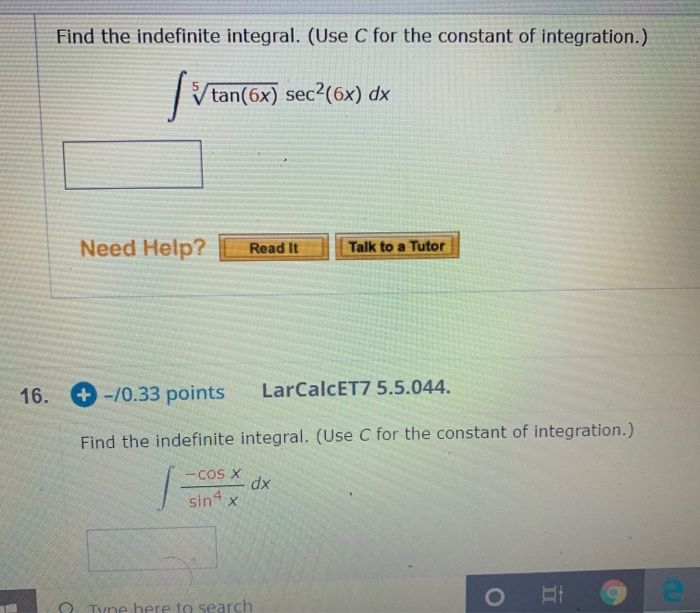
Solved Find The Indefinite Integral Use C For The Constant Chegg Com

Integration Of Tan 2 X Sec 2 X Youtube

Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x

bestpictjcry Tan 2x Tan 2x

Integral Of Sec 2 X Tan 2 X 3tan X 2 Dx Youtube

Integral 1 Tan 2 X Sec 2 X Youtube

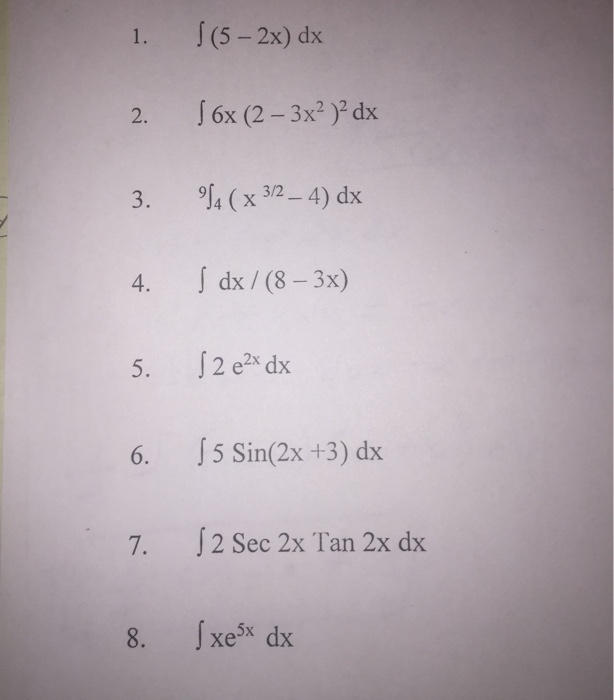
Solved Integral 5 2x Dx Integral 6x 2 3x 2 2 Dx Chegg Com

Misc 32 Definite Integral X Tan X Sec X Tanx Miscellaneous

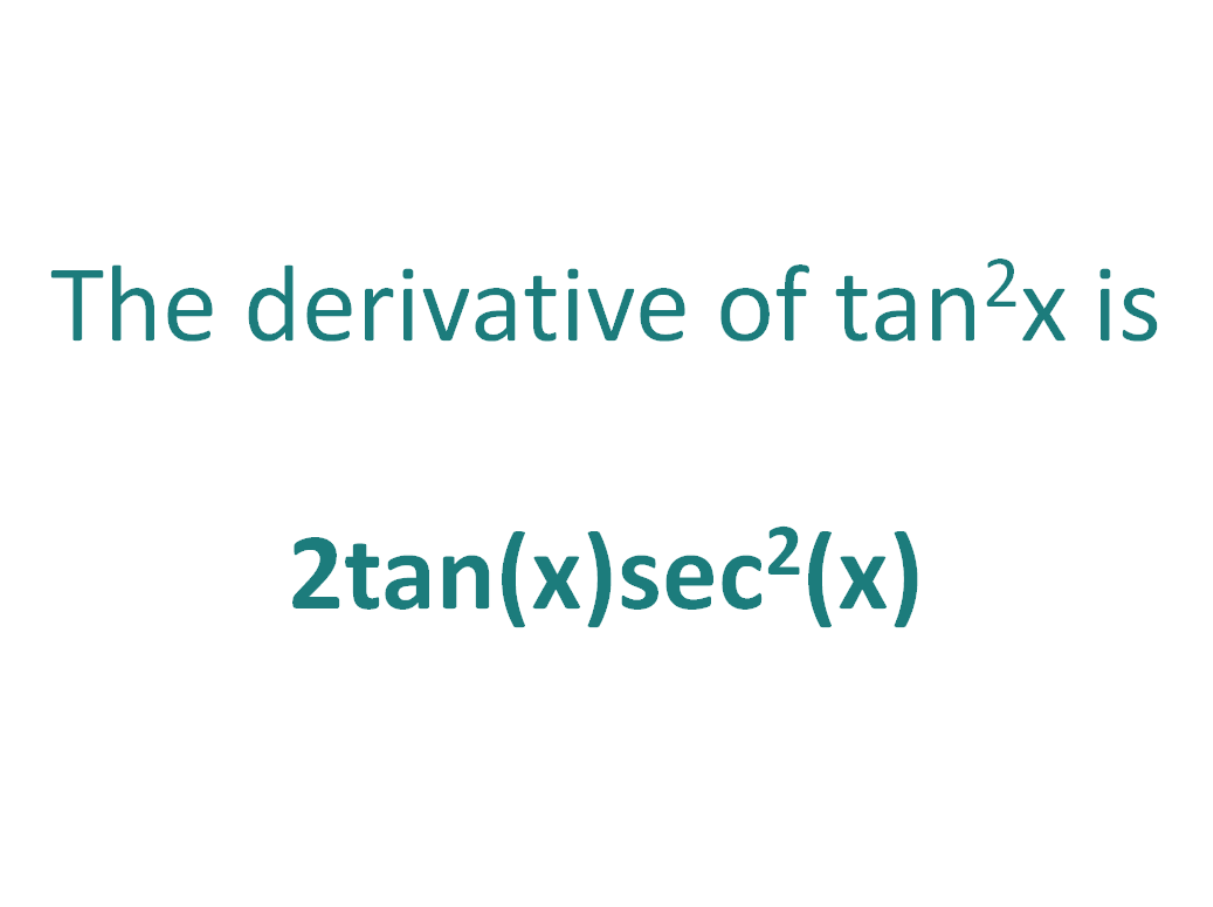
The Derivative Of Tan 2x Derivativeit

2

Integral Of Tan 2x Sec 2x Dx

7 2 Trigonometric Integrals Ppt Download

2

Answered Evaluate The Indefinite Integral Sum Bartleby

How To Integrate 2x Sec 3 X 2 3 Tan X 2 3 Quora

Consider The Function F X Whose Second Derivative Is F X 8x 4sin X If F 0 3 And F 0 4 What Is F 3 Socratic

How To Integrate Math Tan 2 X Sec 6 X Math Using U Substitution Quora

Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x

Integration Calculus Notes

Integral Tan 2 X Sec X Youtube

1

Powers Of Trigonometric Functions

Q28 Tan 2 X Sec 2 X 1 Tan 6 X Dx Integral Of Tan 2 X Sec 2 X 1 Tan 6 X Indefinite Youtube

Integration Calculus Notes

Tan2x Sec2x ただの悪魔の画像

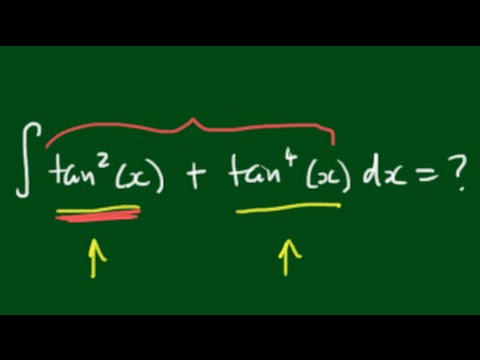
Evaluating The Integral Tan 2 X Tan 4 X Dx Youtube

Int 1 Tan 2x 1 Tan 2x Dx

Integral Of Sec 6 X Tan 2 X Dx

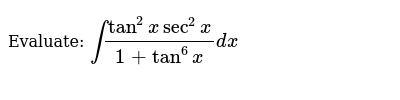
Evaluate Int Tan 2xsec 2x 1 Tan 6x Dx

How To Integrate Math Tan 2 X Sec 6 X Math Using U Substitution Quora

Integrate X Sec 2 2x Dx

Powers Of Trigonometric Functions

Calculus Integration Strategy Trig Tan 6x Sec 4x Even Power Products Youtube

Solved Integral 2x Sec X 2 Tan X 2 Dx Integral Cot Theta D Chegg Com

Int Tan 2x Secx 1 Dx Youtube

Evaluate Int Tan 2xsec 2x 1 Tan 6x Dx

Ncert Solutions For Class 12 Maths Chapter 7 Integers Ex 7 3

Evaluate Int Tan 2xsec 2x 1 Tan 6x Dx

Solved Evaluate Each Of The Following Integrals Using The Chegg Com

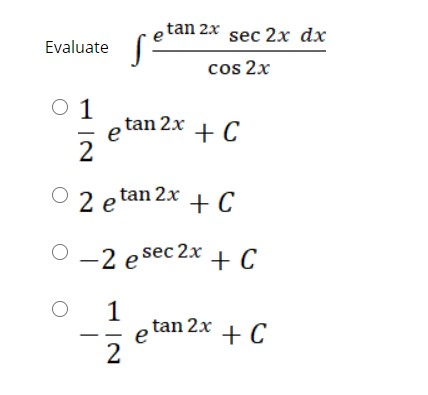
Answered Tan 2x Sec 2x Dx Evaluate Cos 2x O 1 Bartleby

Tan2x Sec2x ただの悪魔の画像

3

Solved Evaluate The Integral Int 0 Pi 3 Tan 5 X Sec 6 X D X

Integral Tan 2x Sec 2x 1 Tan 6x Dx Brainly In

Substitution Rule

bestpictjcry Tan 2x Tan 2x